Comecemos pelo princípio

Quando falamos sobre a taxa de uma reação, queremos dizer a taxa na qual os produtos aparecem. Isso significa que também é igual ao desaparecimento dos reagentes. Portanto, quando quantificamos a taxa em termos de reagentes, eles devem estar em magnitude oposta. $$ \ text {rate} = \ frac {\ Delta [\ text {product}]} {\ Delta t} = - \ frac {\ Delta [\ text {reactant}]} {\ Delta t} $$

De A a B (e C)

Suponha que estou executando a reação $ \ ce {A ->B + C} $ em dois recipientes separados, frasco 1 e frasco 2, cada um com uma concentração diferente de $ \ ce {A} $. Diremos que o frasco 1 é mais concentrado. Se você concorda que a taxa inicial é dada por $ \ text {taxa} _ \ mathrm {i} = k [\ ce {A}] _ \ mathrm {i} $, segue-se que, para cada um, a taxa inicial é $ \ text {taxa} _ {i, fl1} = k [\ ce {A}] _ {i, fl1} $ e $ \ text {taxa} _ {i, fl2} = k [\ ce {A}] _ {i, fl2}, $ respectivamente.

Se adicionássemos algo ao frasco 2, isso mudaria a taxa de reação? Contanto que não adicionássemos nenhum $ \ ce {A}, $ a taxa seria a mesma. A taxa depende de $ \ ce {A} $, mas de nada mais. Então, vamos adicionar um pouco de $ \ ce {B} $ e um pouco de oc $ \ ce {C} $. Vamos adicionar a mesma quantidade de ambos. Vamos chamar esse valor de $ x $ e igualá-lo à diferença de concentração em $ \ ce {A} $ nos dois frascos. $$ x = [\ ce {A}] _ {i, f1} - [\ ce {A}] _ {i.f2} $$

Agora vamos deixar a reação no frasco 1 prosseguir até que a concentração de $ \ ce {A} $ seja igual à quantidade no frasco 2. Para distinguir as condições agora das condições iniciais, chamaremos este tempo de $ t = 1 $ (unidades arbitrárias). Pela estequiometria da reação, sabemos que a quantidade de $ \ ce {A} $ e $ \ ce {A} $ será $ \ Delta [\ ce {A}] = [\ ce {A}] _ {i , f1} - [\ ce {A}] _ {i, f2} = x $ Não há diferença perceptível entre os dois frascos e a taxa de reação é, portanto, a mesma no frasco 1 e no frasco 2. Porque escolhemos concentrações arbitrárias, podemos abstraí-lo para qualquer concentração. $$ \ text {rate} _ {t = 1, f1} = \ text {rate} _ {i, f2} = k [a \ ce {A}] _ {i, f2} = k [\ ce {A }] $$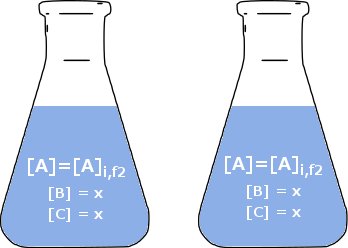

Finalmente, queremos a taxa instantânea. Fazemos isso diminuindo o intervalo de tempo para um valor infinitesimal. $$ \ lim _ {\ Delta t \ a 0} \ frac {- \ Delta [\ ce {A}]} {\ Delta t} = - \ frac {\ mathrm {d} [\ ce {A}]} { \ mathrm {d} t} = k [\ ce {A}] $$

Uma reação de primeira ordem é definida como uma reação em que a taxa de reação obedece à equação $$ r (t) \ equiv \ mathrm {d} [A (t)] / \ mathrm {d} t = k [A (t)] \ tag {1} $$ Sua primeira equação $$ r (0) \ equiv \ mathrm {d} [A (0)] / \ mathrm {d} t = k [A (0)] \ tag {2} $$

é apenas uma situação particular. Não podemos saber a priori se uma reação que obedece a (2) obedecerá a (1). Só podemos medir como $ r (t) $ varia ao longo do tempo. Se $ r (t) $ segue a equação (1), então é dito que a cinética segue uma equação de primeira ordem.

Em reações químicas do tipo $ \ ce {A -> B + C} $ é natural esperar uma reação de primeira ordem nos tempos iniciais. Contanto que a reação não precise de nenhuma outra molécula ou agente no meio (além de talvez outros fatores essencialmente constantes) do que $ \ ce {A} $, e não envolva colisões entre duas ou mais moléculas para iniciar a reação , pode-se esperar que a taxa seja proporcional ao número de moléculas presentes em cada momento, portanto, para $ [\ ce {A} (t)] $.

Depois de um longo tempo, quando a concentração reativa é esgotada e a concentração dos produtos aumenta (assumindo que não há difusão dos produtos) a lei de primeira ordem é normalmente violada, uma vez que a reação de retorno $ \ ce {B + C -> A} $ (além de outras colisões) pode ocorrer . Em particular, não é possível alcançar condições de equilíbrio sob a lei de primeira ordem.